数学初高中衔接——比例性质的七个公式

4个非零数，a、b、c、d，如果a：b=c：d（或改写成=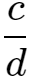）ad=bc。其中，a、d叫做比例外项，b、c叫做比例内项，d叫做a、b、c的第四比例项。如果两个比例内项相等，即a：b=b：c，此时把b叫做a和c的比例中项。

比例的基本性质：a：b=c：d（或改写成=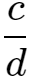）ad=bc，（bd≠0）比例的两个外项的乘积等于两个内项的乘积。

更比定理：ad=bc，可以写成bc=ab，ad=cb，cb=da等形式。

合比定理：如果a：b=c：d，（a±b）：b=（c±d）/d。

等比定理（等比性质）：如果a：b=c：d=m：n（b+d+…+n≠0），（a+c+m）：（b+d++n）=a：b。

例题1：已知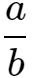===4，b+d+f=5，求a+c+e的值。

解：因为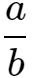===4，则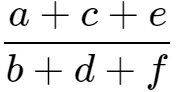=4，所以a+c+e=4（b+d+f）=4×5=20.

例题2：已知a∶b∶c=2∶3∶4，且2a+b-c＝6，则a-b+2c=（ 14）

解：设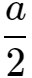==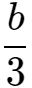=k，则a=2k，b=3k，c=4k，2a+b-c＝2×2k+3k-4k=3k=6，k=2，得出a＝4，b＝6 ，c＝8，所以a-b+2c=4-6+2×8=14

例题3：已知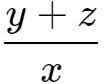==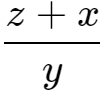,则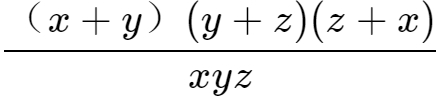=( -1,或8 )